Gains from Trade through Compromise
First written: 26 July 2013; last update: 18 Feb. 2018
When agents of differing values compete for power, they may find it mutually advantageous in expectation to arrive at a compromise solution rather than continuing to fight for winner takes all. I suggest a few toy examples of future scenarios in which suffering reducers could benefit from trade. I propose ideas for how to encourage compromise among nations, ideologies, and individuals in the future, including moral tolerance, democracy, trade, social stability, and global governance. We should develop stronger institutions and mechanisms that allow for greater levels of compromise.
Other versions
Contents
- Introduction
- Another compromise scenario
- Power-based valuation for compromises
- It's not about you
- Why don't we see more compromise?
- Iterated prisoner's dilemmas
- Agents that prefer not to compromise
- Light-speed limits to negotiation
- Ideas for encouraging more cooperation
- Epistemic disagreements
- What about moral advocacy?
- Words vs. actions
- Compromise as a market
- Values as vectors
- Working together on compromise
- Acknowledgements
- Appendix: Dividing the compromise pie
- Footnotes
Introduction
"Any man to whom you can do favor is your friend, and [...] you can do a favor to almost anyone."
--Mark Caine
"Gains from trade" in economics refers to situations where two parties can engage in cooperative behavior that makes each side better off. A similar concept applies in the realm of power struggles between competing agents with different values. For example, consider the following scenario.
Deep ecologists vs. animal welfarists. Imagine that two ideologies control the future: Deep ecology and animal welfare. The deep ecologists want to preserve terrestrial ecosystems as they are, including all the suffering they contain. (Ned Hettinger: "Respecting nature means respecting the ways in which nature trades values, and such respect includes painful killings for the purpose of life support.") The animal welfarists want to intervene to dramatically reduce suffering in the wild, even if this means eliminating most wildlife habitats. These two sides are in a race to control the first artificial general intelligence (AGI), at which point the winner can take over the future light cone and enforce its values.
Suppose the two sides are equally matched in resources: They each have a 50% shot at winning. Let's normalize the values for each side between 0 and 100. If the deep ecologists win, they get to preserve all their beloved ecosystems; this outcome has value 100 to them. If they lose, their ecosystems disappear, leaving 0 value. Meanwhile, the values are swapped for the animal welfarists: If they win and eliminate the suffering-filled ecosystems, they achieve value 100, else the value to them is 0. Since the chance of each side winning is 50%, each side has an expected value of 50.
But there's another option besides just fighting for winner takes all. Say the deep ecologists care more about preserving species diversity than about sheer number of organisms. Maybe they're also more interested in keeping around big, majestic animals in their raw form than about maintaining multitudes of termites and cockroaches. Perhaps some ecologists just want the spectacle of wildlife without requiring it to be biological, and they could be satisfied by lifelike robot animals whose conscious suffering is disabled at appropriate moments, such as when being eaten.1 Maybe others would be okay with virtual-reality simulations of Earth's original wildlife in which the suffering computations are skipped over in the virtual animals' brains.
These possibilities suggest room for both parties to gain from compromise. For instance, the animal welfarists could say, "We want to get rid of 60% of suffering wild animals, but we'll eliminate the ones that you care about least (e.g., insects when they're not crucial for supporting the big animals), and we'll keep some copies of everything to satisfy your diversity concerns, along with doing some robots and non-suffering simulations." Maybe this would be ~60% as good as complete victory in the eyes of the deep ecologists. If the two sides make this arrangement, each gets value 60 with certainty instead of expected value 50.
Here, there were gains from trade because the animal welfarists could choose for the compromise those methods of reducing wild-animal suffering that had least impact to the deep ecologists' values. In general, when two sets of values are not complete polar opposites of each other, we should expect a concave-down curve like the red one below illustrating the "production possibilities" for the two values. When the curve is concave down, we have possible gains from trade relative to duking it out for winner takes all (blue line). The blue line illustrates the expected value for each value system parameterized by the probability in [0,1] for one of the value systems winning.
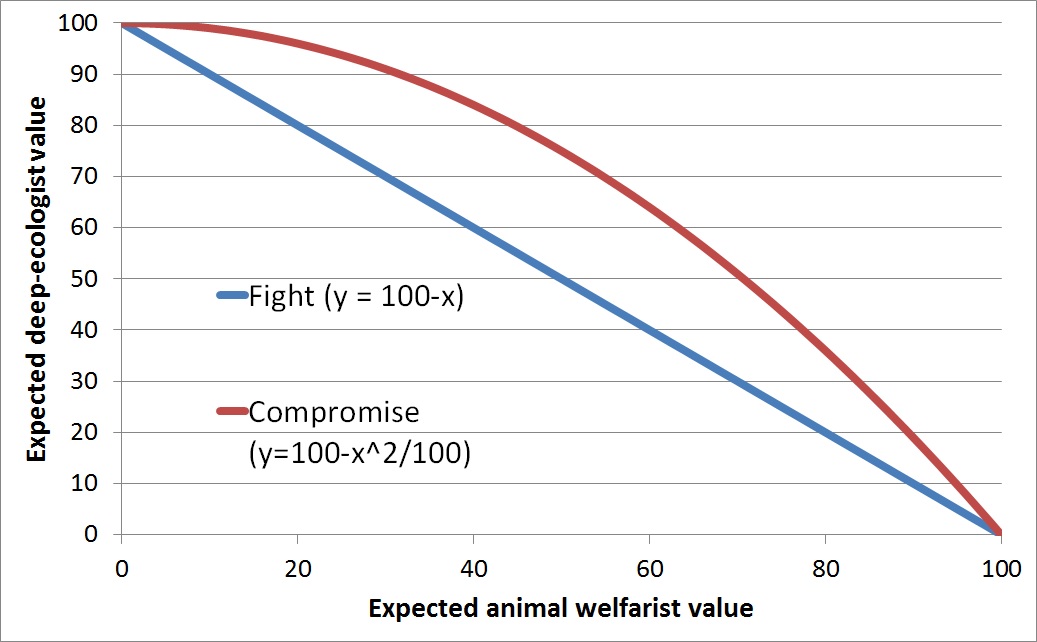
Figure 1: Fight vs. compromise for deep ecologists vs. animal welfarists.
Another compromise scenario
We can imagine many additional examples in which suffering reducers might do better to trade with those of differing value systems rather than fight for total control. Here's one more example to illustrate:
- Suffering subroutines for profit. Suppose a robotics company trains its robotic minions using a reinforcement-learning algorithm that is extremely effective but also causes conscious suffering to the robots. Robot welfarists protest for a law to ban use of this painful algorithm. The debate in the legislature is long and fierce. Eventually, the two sides reach a compromise: The algorithm may still be used, but only in cases where the company presents a clear need to an ethics committee. This results in a substantial reduction in the company's use of suffering robots without precluding their utilization in the most crucial instances. (Compare to present-day animal-testing disputes. A similar scenario would have worked in the case of researchers doing psychological experiments on conscious artificial minds.)
Power-based valuation for compromises
In these disputes, the relevant variable for deciding how to slice the compromise seems to be the probability that each side would win if it were to continue fighting in an all-or-nothing way. These probabilities might be roughly proportional to the resources (financial, political, cultural, technological, etc.) that each side has, as well as its potential for growth. For instance, even though the movement to reduce wild-animal suffering is small now, I think it has potential to grow significantly in the future, so I wouldn't make early compromises for too little in concessions.
This is analogous to valuation of startup companies: Should the founders sell out or keep going in case they can sell out for a higher value later? If they do badly, they might actually get less. For instance, Google offered to buy Groupon for $5.75 billion in 2010, but Groupon turned down the offer, and by 2012, Groupon's market cap fell to less than $5.75 billion.
In "Rationalist explanations for war," pp. 386-87, James D. Fearon makes this same observation: Two states with perfect information should always prefer a negotiation over fighting, with the negotiation point being roughly the probability that each side wins.
I discuss further frameworks for picking a precise bargaining point in "Appendix: Dividing the compromise pie."
Our social intuitions about fairness and democracy posit that everyone deserves an equal say in the final outcome. Unfortunately for these intuitions, compromise bargains are necessarily weighted by power -- "might makes right." We may not like this fact, but there seems no way around it. Of course, our individual utility functions can weight each organism equally, but in the final compromise arrangement, those with more power get more of what they want.
It's not about you
Many people care about complexity, diversity, and a host of other values that I don't find important. I have significant reservations about human space colonization, but I'm willing to let others pursue this dream because they care about it a lot, and I hope in return that they would consider the need to maintain safeguards against future suffering. The importance of compromise does not rely on you, in the back of your mind, giving some intrinsic moral weight to what other agents want; compromise is still important even when you don't care in the slightest or may even be apprehensive about the goals of other factions. To appropriate a quote from Noam Chomsky: If we don't believe in strategic compromise with those we can't identify with, we don't believe in it at all.
Why don't we see more compromise?
If this compromise approach of resolving conflicts by buying out the other side worked, why wouldn't we see it more often? Interest groups should be compromising instead of engaging in zero-sum campaigns. Countries, rather than going to war, could just assess the relative likelihood of each side winning and apportion the goods based on that.
Even animals shouldn't fight: They should just size up their opponents, estimate the probability of each side winning, and split the resources appropriately. In the case of fighting animals, they could get the same expected resources with less injury cost. For instance, two bull seals fighting for a harem of 100 cows, if they appear equally matched, could just split the cows 50-50 and avoid the mutual fitness costs of getting injured in the fight.
Here are a few possibilities why we don't see more cooperation in animals, but I don't know if they're accurate:
- The adaptation is too hard to reach by evolution,2 maybe because accurately estimating the probability of each side winning is harder than just trying the fight to see who wins. Maybe the estimates would also become untrustworthy over time without feedback to reinforce their tracking of truth.
- Maybe different sides have different probabilities for who would win and so can't agree on a mutual split. (But Bayesian agents who take seriously the modesty argument for epistemic priors might not have this problem? Though I guess each side might have incentives to deceive the other about its ability.)
- Maybe it does happen more than we think, but we only see the cases where this kind of trade breaks down. There's plenty showing off your size to scare down the other guy and other non-violent forms of intimidation. The conflicts might just be cases where this "trade rather than fight" approach stops working.
Of course, there are plenty of examples where animals have settled on cooperative strategies. It's just important to note that they don't always do so, and perhaps we could generalize under what conditions cooperation breaks down.
Human wars often represent a failure of cooperation as well. While wars sometimes have "irrational" causes, Matthew O. Jackson and Massimo Morelli argue in "The Reasons for Wars - an Updated Survey" that many can be framed in rationalist terms, and they cite five main reasons for the breakdown of negotiation. An exhaustive survey of theories of war is contained in a syllabus by Jack S. Levy.
How about in intra-state politics? There are plenty of compromises there, but maybe not as many as one might expect. For instance, Toby Ord proposed in 2008:
It is so inefficient that there are pro- and anti- gun control charities and pro- and anti-abortion charities. Charities on either side of the divide should be able to agree to 'cancel' off some of their funds and give it to a mutually agreed good cause (like developing world aid). This would do just as much for (or against) gun control as spending it on their zero-sum campaigning, as well as doing additional good for others.
A similar idea was floated on LessWrong in 2010. I have heard of couples both not voting because they'd negate each other, but I haven't heard of an organization as described above for cancelling opposed donations. Why hasn't something like this taken off?
- Maybe, like in the case of animals, social evolution just hasn't gotten to it yet.
- Each side may be overconfident in its own effectiveness per dollar relative to the other, or at least wants to pretend that it's highly confident in its effectiveness over the other side.
- Maybe one side is actually more effective per dollar, but the less effective side doesn't want to admit this by using a ratio other than 1:1 for donation cancellation.
- Maybe the work that a pro-choice organization does isn't exactly cancelled by the work of a pro-life organization. For instance, Planned Parenthood provides a lot of services to people in addition to doing political lobbying.
- On LessWrong, patrissimo suggests that political donations may sometimes be more about signaling affiliation rather than about actually changing policy.
Whatever the reason is that we don't see more cancelling of opposed political forces, the fact remains that we do see a lot of compromise in many domains of human society, including legislation (I get my provision if you get yours), international relations (we'll provide weapons if you fight people we don't like), business (deals, contracts, purchases, etc.), and all kinds of social relations (Brother Bear will play any three games with Sister Bear if she plays Space Grizzlies with him later). And we're seeing an increasing trend toward positive-sum compromise as time goes on.
Iterated prisoner's dilemmas
While racing to control the first AGI amounts to a one-shot prisoner's dilemma, most of life's competitive scenarios are iterated. Indeed, even in the case of AGI arms race, there are many intermediate steps along the way where the parties choose cooperation vs. defection, such as when expanding their resources. Iterated prisoner's dilemmas provide a very strong basis for cooperation, as was demonstrated by Robert Axelrod's tournaments. As the Wikipedia article explains:
In summary, success in an evolutionary "game" correlated with the following characteristics:
- Be nice: cooperate, never be the first to defect.
- Be provocable: return defection for defection, cooperation for cooperation.
- Don't be envious:: be fair with your partner.
- Don't be too clever: or, don't try to be tricky.
Iterated prisoner's dilemmas yielded cooperation in an evolutionary environment with no pre-existing institutions or enforcement mechanisms, and the same should apply even in those iterated prisoner's dilemmas between groups today where no formal governing systems are yet in place. In this light, it seems suffering reducers should put out their compromise hand first and aim to help all values in a power-weighted fashion, at least to some degree, and then if we see others aren't reciprocating, we can temporarily withdraw our assistance.
Agents that prefer not to compromise
One can imagine agents for whom compromise is actually not beneficial because they have increasing rather than diminishing returns to resources. In the "Introductory example," we saw that both animal welfarists and deep ecologists had diminishing returns with respect to how much control they got, because they could satisfy their most important concerns first, and then later concerns were less and less important. Imagine instead an agent that believes that the value of a happy brain is super-linear in the size of that brain: e.g., say the value is quadratic. Then the agent would prefer a 50% chance of getting all the matter M in the future light cone to produce a brain with value proportional to M2 rather than a guarantee of getting half of the matter in the universe to produce a brain with value proportional to (M/2)2 = M2/4. I think agents of this type are rare, but we should be cautious about the possibility.
Sacred values
Another interesting case is that of sacred values. It seems that offering monetary compensation for violation of a sacred value actually makes people more unwilling to compromise. While we ordinarily imagine sacred values in contexts like the abortion debate or disputes over holy lands, they can even emerge for modern issues like Iran's nuclear program. Philip Tetlock has a number of papers on sacred-value tradeoffs.
It seems that people are more willing to concede on sacred values in return for other sacred values, which means that compromise with such people is not hopeless but just requires more than a single common currency of exchange.
Light-speed limits to negotiation
Bargaining on Earth is fast, reliable, and verifiable. But what would happen in a much bigger civilization that spans across solar systems and galaxies?
Intergalactic democracy?
The Virgo Supercluster is 110 million light-years in diameter. Suppose there was an "intergalactic federation" of agents across the Virgo Supercluster that met at a Congress at the center of the supercluster. The galaxies could transmit digital encodings of their representatives via radar, which would take 55 million years for the most distant regions. The representatives would convene, reach agreements, and then broadcast back the decisions, taking another 55 million years to reach the destination galaxies. This process would be really slow, especially if the digital minds of the future run at extremely high speeds. Still, if we had, say, 1012 years before dark energy separated the parts of the supercluster too far asunder, we could still get in 1012/108 = 10,000 rounds of exchanges. (As Andres Gomez Emilsson pointed out to me, this calculation doesn't count the expansion of space during that time. Maybe the actual number of exchanges would be lower on this account.) In addition, if the galaxies dispatched new representatives before the old ones returned, they could squeeze in many more rounds, though with less new information at each round.
Is cross-supercluster communication feasible?
Would it even be possible to transmit radar signals across the 55 million light-years? According to Table 1 of "How far away could we detect radio transmissions?," most broadband signals can travel just a tiny fraction of a light-year. S-band waves sent at high enough EIRP could potentially travel hundreds of light-years. For instance, the table suggests that at 22 terawatts of transmission EIRP, the detection range would be 720 light-years.
In the 1970s, humanity as a whole used ~10 terawatts, but the sun produces 4 * 1014 terawatts, so maybe 22 terawatts is even conservative. The detection range is proportional to the square root of EIRP, so multiplying the detection range by 10 requires multiplying EIRP by 100. Obviously hundreds or thousands of light-years for radar transmission is tiny compared with 55 million light-years for the intergalactic distances at hand, but the communication can be routed from one star to the next. There are "rogue" intergalactic stars that might serve as rest stops, but whether they would be able to be located and whether they would all be within a few thousand light-years of each other is unclear. Perhaps custom-built probes could relay messages from one node to the next across large interstellar distances, creating an intergalactic equivalent of the Internet.
Intergalactic communication is easier than intergalactic travel for material structures (e.g., the initial von Neumann probes that would do the colonizing). If solutions were found for intergalactic travel (e.g., speculative faster-than-light scenarios), these would aid in intergalactic compromise as well.
Verification
Even if you can make deals every 110 million years, how do you verify that the distant regions are following up on their sides of the bargains? Maybe the different factions (e.g., deep ecologists vs. animal welfarists) could build monitoring systems to watch what the others were doing. Representatives from all the different factions could be transmitted back from Congress to the home galaxies for follow-up inspections. But what would keep the home galaxies from just destroying the inspectors? Who would stop them? Maybe the home galaxies would have to prove at the next Congress session that they didn't hamper the inspectors, but it's not at all clear it would be possible to verify that.
What might work better would be if each home galaxy had a proportionate balance of parties from the different factions so that they would each have the power to keep the other sides in check. For example, if there were lots of deep ecologists and animal welfarists in both galaxies, most of the compromise could be done on a local scale, the same as it would be if intergalactic communication didn't exist. A risk would be if some of the local galaxies devolved into conflict in which some of the parties were eliminated. Would the other parts of the supercluster be able to verify that this had happened? And even if so, could a police force rectify the situation?
Compromise before spreading
 Cross-supercluster communication seems tricky. Probably most of the exchanges among parties would happen at a local level, and intergalactic trades might be a rare and slow process.
Cross-supercluster communication seems tricky. Probably most of the exchanges among parties would happen at a local level, and intergalactic trades might be a rare and slow process.
The easiest time to "divide up our future light cone" among competing factions seems to be at the beginning, before we send out the first von Neumann probes. Either different factions would be allocated different portions of the universe into which to expand, or all parties would agree upon a compromise payload to spread uniformly. This latter solution would prevent attempts to cheat by colonizing more than your fair share.
Of course, we would still need to compromise with aliens if we encountered them, but among (post-)humans, maybe all the compromise could be done at the beginning.
However, the idea of finding a perfect compromise at the beginning of colonization that continues working forever assumes that reliable goal preservation is possible, even for rapidly changing and learning digital agents that will persist for billions of years. That level of goal preservation seems very tricky to achieve in artificial general intelligences, which are extremely complex systems. So there might inevitably be divergence in beliefs and values among non-communicating galaxies, and this could eventually lead to conflicts.
Galactic compromise is easier than intergalactic
Note that merely galactic democracy would be less challenging. The Milky Way is only 100,000 light-years in diameter, and I would guess that most of the stars are within thousands of light-years of each other, so networked radar transmission should be feasible. Congressional cycles would take only 100,000 years instead of 110 million. And the number of stars is not that small: maybe 100 to 400 billion, compared with about 200 trillion in the whole Virgo Supercluster. This is just a factor-of-103 difference and so shouldn't affect our expected-value calculations too much. In other words, intergalactic bartering isn't necessary for compromise on cosmic scales to still be important.
Ideas for encouraging more cooperation
See "Possible Ways to Promote Compromise." We should evaluate the effectiveness and efficiency of these approaches and explore other ways forward.
Epistemic disagreements
In this essay I've focused on value disagreements between factions, and there's a reason for this. Facts and values are fundamentally two separate things. Values are things you want, drives to get something, and hence they differ from organism to organism. Facts are descriptions about the world that are true for everyone at once. Truth is not person-dependent. Even if post-modernists or skeptics are right that truth is somehow person-dependent or that there is no such thing as truth, then at least this realization is still true in some meta-level of reasoning, unless even this is denied, but such a view is rare, and such people are presumably not going to be doing much to try to shape the world.
Epistemic convergence
Given that there is some external truth about the universe, different people can share ideas about it, and other people's beliefs are evidence relevant to what we ourselves should believe. "Person A believes B" is a fact about the universe that our theories need to explain.
We should keep in mind that our Bayesian priors were shaped by various genetic and environmental factors in our development, and if we had grown up with the circumstances of other people, we would hold their priors. In some cases, it's clear that one set of priors is more likely correct -- e.g., if one person grew up with major parts of his brain malfunctional, his priors are less likely accurate than those of someone with a normal brain, and one reason for thinking so is that humans' normal brain structure has been shaped by evolution to track truths about the world, whereas random modifications to such a brain are less likely to generate comparably accurate views. In this case, both the normal brain and the malfunctional brain should agree to give more weight to the priors of the normal brain, though both brains are still useful sources of data.
Even in cases where there's no clear reason to prefer one brain or another, it seems both brains should recognize their symmetry and update their individual priors to a common prior, as Robin Hanson suggests in "Uncommon Priors Require Origin Disputes." This is conceptually similar to two different belief impulses within your own brain being combined into a common belief via dissonance-resolution mechanisms. It's not specified how the merging process takes place -- it's not always an average, or even a weighted average, of the two starting points, but it seems rationally required for the merge to happen. Then, once we have common priors, we should have common posteriors by Aumann's theorem.
Caveats
There are caveats in order.
- Limited computation: The actual process of belief resolution takes time and effort, and it's probably impossible for two people to completely converge given present-day computational resources. However, we can make crude approximations in the short term, before full resolution is hashed out. We can increase our uncertainty when other smart people disagree with us on factual questions, ask them why, and move some in their direction, especially if they do the same with us.
- Disagreement about agreement: Not everyone agrees that we should have common priors. Indeed, many people don't even accept the Bayesian framework within which this thinking is cast. For example, presuppositionalists and fideists would assert that we can have justification for our beliefs purely from other sources like the Bible or just faith independent of any attempted grounding.3 Even atheist Bayesians sometimes demur at the prospect of the rational requirement for epistemic convergence. This presents a challenge to my hope that factual disagreements are less severe than moral ones, and it suggests that in addition to the interventions discussed above for promoting moral compromise, we might also advance the arguments for epistemic compromise, in order to reduce (what I think are) misguided conflicts that should be fought in the realm of ideas rather than in the realm of zero-sum actions, like political lobbying based on facts that you think you know better than the other side.
I have some hope that very rational agents of the future will not have much problem with epistemic disagreements, because I think the argument for epistemic modesty is compelling, and most of the smartest people I know accept it, at least in broad outline. If evolutionary pressures continue to operate going forward, they'll select for rationality, which means those practicing epistemic modesty should generally win out, if it is in fact the right stance to take. Thus, I see value conflicts as a more fundamental issue in the long run than factual ones.
That said, many of the conflicts we see today are at least partially, and sometimes primarily, about facts rather than values. Some debates in politics, for instance, are at least nominally about factual questions: Which policy will improve economic growth more? Are prevention measures against climate change cost-effective? Does gun control reduce violent crime? Of course, in practice these questions tend to become ideologized into value-driven emotional issues. Similarly, many religious disputes are at least theoretically factual -- What is/are the true God/gods? What is His/Her/their will for humanity? -- although, even more than in politics, many impulses on these questions are driven by emotion rather than genuine factual uncertainty. It's worth exploring how much rationality would promote compromise in these domains vs. how much other sociological factors are the causes and hence the best focal points for solutions.
Divergences among effective altruists
There are disagreements in the effective-altruism movement about which causes to pursue and in what ways. I think many of the debates ultimately come down to value differences -- e.g., how much to care about suffering vs. happiness vs. preferences vs. other things, whether to care about animals or just humans and how much, whether to accept Pascalian gambles. But many other disagreements, especially in the short term, are about epistemology: How much can we grapple with long-term scenarios vs. how much should we just focus on short-term helping? How much should we focus on quantified measurement vs. qualitative understanding? How much should we think about flow-through effects?
Some are concerned that these differences in epistemology are harmful because they segregate the movement. I take mostly the opposite view. I think it's great to have lots of different groups trying out lots of different things. This helps you learn faster than if you all agreed on one central strategy. There is some risk of wasting resources on zero-sum squabbles, and it's good to consider cases where that happens and how to avoid them. At the same time, I think competition is also valuable, just as in the private sector. When organizations compete for donors using arguments, they improve the state of the debate and are forced to make the strongest case for their views. (Of course, recruiting donors via other "unfair" means doesn't have this same property.) While it might help for altruists to become better aligned, we also don't want to get comfortable with just averaging our opinions rather than seeking to show why our side may actually be more correct than others supposed.
Convergence should not lead to uniformity
This discussion highlights a more general point. Sometimes I feel epistemic modesty is too often cited as an empty argument: "Most smart people disagree with you about claim X, so it's probably wrong." Of course, this reasoning is valid, and it's important for everyone to realize as much, but this shouldn't be the end of the debate. There remains the task of showing why X is wrong at an object level. Analogously, we could say, "Theorem Y is true because it's in my peer-reviewed textbook," but it's a different matter to actually walk through the proof and show why theorem Y is correct. And every once in a while, it'll turn out that theorem Y is actually wrong, perhaps due to a typographical error or, in rare occasions, due to a more serious oversight by the authors. Intellectual progress comes from the latter cases: investigating a commonly held assumption and eventually discovering that it wasn't as accurate as people had thought.
Most new ideas are wrong. For every Copernicus or Galileo there are hundreds of scientists who are misguided, confused, or unlucky in interpreting their experimental findings. But we have to not be satisfied with conventional wisdom, and we have to actually look at the details of why others are wrong in order to make progress. It's plausible that an epistemically diverse population leads to faster learning than a uniform one. If startup founders weren't overconfident, we'd have fewer startups and hence less economic growth. Similarly, if people are less confident in their theories, they might push them less hard, and society might have less intellectual progress as a result.
However, epistemic divergence can be harmful in cases where each party can act on its own and thereby spoil the restraint of everyone else; Bostrom et al. call this the "The Unilateralist’s Curse". In these cases, it's best if everyone adheres to a policy of epistemic modesty. In general, maybe the ideal situation is for people to hold approximately uniform actual beliefs but then play advocate for a particular idea that they'd like to see explored more, even though it's probably wrong. There are times when I do this: propose something that I don't actually think is right, because I want to test it out.
While fighting over conflicting beliefs is not a good idea, groupthink is a danger in the reverse direction. While groups are collectively more accurate than individuals on average, when a group's views are swayed by conformity to each other or a leader, these accuracy benefits diminish. Groups with strong norms encouraging everyone to speak her own mind and rewarding constructive criticism can reduce groupthink.
Epistemic prisoner's dilemma
Another reason why I sometimes make stronger statements than I actually believe is a sort of epistemic prisoner's dilemma.4 In particular, I often feel that other people don't update enough in response to the fact that I believe what I do. If they're not going to update in my direction, I can't update in their direction, because otherwise my position would be lost, and this would be worse than us both maintaining our different views.
For example, say Alice and Bob both have beliefs about some fact, like the number of countries in the world. Alice thinks the number is around 180; Bob thinks it's around 210. The best outcome would be for both parties to update in each other's directions, yielding something like 195, which is actually the number of independent states recognized by the US Department of State. However, say Alice is unwilling to budge on her estimate. If Bob were to move in her direction -- say part way, to 195 -- then Bob's views would be more accurate, but on collective decisions made by the Alice/Bob team, the decisions would, through their tug of war, be centered on something like (180+195)/2 = 187.5, which is farther from the truth than the collective decisions made by Alice/Bob holding 180 and 210 as their beliefs. In other words, if the collective decision-making process itself partly averages Alice's and Bob's views, then Bob should hold his ground as long as Alice holds her ground, even if this means more friction in the form of zero-sum conflicts due to their epistemic disagreement.
If Alice and Bob are both altruists, then this situation should be soluble by each side realizing that it makes sense to update in the other's direction. There's not an inherent conflict due to different payoffs to each party like in the regular prisoner's dilemma.
In general, epistemic compromise is similar to game-theoretic compromise in that it makes both parties better off, because both sides in general improve their beliefs, and hence their expected payoffs, in the process of resolving disagreement. Of course, if the agents have anticorrelated values, there can be cases where disagreement resolution is net harmful to at least one side, such as if a terrorist group resolves its factual disagreement with the US government about which method of making dirty bombs is most effective. By improving the factual accuracy of the terrorists, this may have been a net loss for the US government's goals.
What about moral advocacy?
When is moral activism a positive-sum activity for society, and when does it just transfer power from one group to another? This is a complex question.
Consider the case of an anti-death-penalty activist trying to convince people who support the death penalty that this form of punishment is morally wrong. Naively we might say, "Some people support the death penalty, others oppose it, and all that's going on here is transferring support from one faction to the other. Hence this is zero-sum."
On the other hand, we could reason this way instead: "Insofar as the anti-death-penalty activist is successful, she's demonstrating that the arguments against the death penalty are convincing. This is improving society's wisdom as people adopt more informed viewpoints. Most people should favor more informed viewpoints, so this is a win by many people's values, at least partially." The extent to which this is true depends on how much the persuasion is being done via means that are seen as "legitimate" (e.g., factual evidence, philosophical logic, clear thought experiments, etc.) and how much it's being done via "underhanded" methods (e.g., deceptive images, pairing with negative stimuli, ominous music, smear tactics, etc.). Many people are glad to be persuaded by more legitimate means but resistant to persuasion by the underhanded ones.
So there's a place for moral advocacy even in a compromise framework: Insofar as many factions welcome open debate, they win when society engages in moral discourse. When you change the opinion of an open-minded person, you're doing that person a service. Think of a college seminar discussion: Everyone benefits from the comments of everyone else. Other times moral persuasion may not be sought so actively but is still not unwelcome, such as when people distribute fliers on the sidewalk. Given that the receivers are voluntarily accepting the flier and open to reading it, we'd presume they place at least some positive value on the activity of the leafleter (although the value could be slightly negative if the person accepts the leaflet only due to social pressure). Of course, even if positive, moral persuasion might be far from optimal in terms of how resources are being used; this depends on the particulars of the situation -- how much the agents involved benefit from the leafleting.
However, not everyone is open to persuasion. In some instances a person wants to keep his values rigid. While this may seem parochial, remember that sometimes all of us would agree with this stance. For example: "If you offered Gandhi a pill that made him want to kill people, he would refuse to take it, because he knows that then he would kill people, and the current Gandhi doesn't want to kill people." Being convinced by underhanded means that we should kill people is a harm to our current values. In these cases, underhanded persuasion mechanisms are zero-sum because the losing side is hurt as much as the winning side is helped. Two opposed lobby groups using underhanded methods would both benefit from cancelling some of each other's efforts and directing the funds to an agreed upon alternate cause instead. On the other hand, opposed lobby groups that are advancing the state of the debate are doing a service to society and may wish to continue, even if they're in practice cancelling each other's effects on what fraction of people adopt which stance in the short run.
If changing someone's beliefs against his wishes is a harm to that person, then what are we to make of the following case? Farmer Joe believes that African Americans deserve to be slaves and should not have Constitutional rights. Furthermore, he doesn't want to have his views changed on this matter. Is it a harm to persuade Joe, even by purely intellectual arguments, that African Americans do in fact deserve equal rights? Well, technically yes. Remember that what persuasion methods count as "legitimate" vs. "underhanded" is in the eye of the hearer, and in this case, Joe regards any means of persuasion as underhanded. That said, if Joe were to compromise with the anti-slavery people, the compromise would involve everyone being 99+% against slavery, because in terms of power to control the future, the anti-slavery camp seems to be far ahead. Alternatively, maybe the anti-slavery people could give Joe something else he wants (e.g., an extra couple of shirts) in return for his letting them persuade him of the anti-slavery stance. This could be a good trade for Joe given his side's low prospects of winning in the long run.
As this example reminds us, the current distribution of opinion is not necessarily the same as the future distribution of power, and sometimes we can anticipate in which directions the trends are going. For example, it seems very likely that concern for animal wellbeing will dramatically increase in the coming decades. Unlike the stock market, the trajectory of moral beliefs is not a random walk.
Words vs. actions
Above we saw that moral discourse can often be a positive-sum activity insofar as other parties welcome being persuaded. (Of course, it may not always be as positive-sum as other projects that clearly benefit everyone, such as promoting compromise theory and institutions.) Conflicts in the realm of ideas are usually a good thing.
In contrast, direct actions may be more zero-sum when there's disagreement about the right action to take. Say person A thinks it's good to do a given action, and person B thinks it's equally wrong to do that same action.
While people often complain about "all talk and no action," in some cases, it can be Pareto-better to talk than to take action, if the issue at hand is one under dispute.
Often our actions meld with our beliefs about what's right, so it can sometimes get tricky, if you're trying to adopt a compromise stance for your actions, to mentally separate "how I'm acting for instrumental reasons" with "how I feel for intrinsic reasons." Sometimes people may begin to think of the compromise stance as intrinsically the "right" one, while others will continue to maintain this separation. In our own brains, we can feel the distinction between these two categories with respect to our evolutionary drives: Instrumental reciprocity feels like our moral sense of fairness, and our intrinsic survival drives feel like selfish instincts.
Compromise as a market
Control of Earth's future light cone is something that most value systems want:
- Egoists would like to run eudaimonic simulations of themselves.
- Fun theorists would like to create minds exploring constantly harder challenges.
- Negative utilitarians would like to use computational resources to explore ways to reduce suffering in the universe.
- Complexity maximizers would like to see a melange of interesting digital and physical patterns.
- ...
Each of these value systems can be regarded like an individual in an economy, aiming to maximize its own utility. Each egoist has a separate goal from other egoists, so most of the individuals in this economy might be egoists, and then there would be a few other (very large) individuals corresponding to the fun theorists, utilitarians, complexity maximizers, etc. Resources in this economy include stars, raw materials for building Dyson swarms, knowledge databases, algorithm source code, etc., and an individual's utility derives from using resources to produce what it values.
It's possible that the future will literally contain many agents with divergent values, but it's also possible that just one of these agents will win the race to build AI first, in which case it would have the light cone to itself. There are two cases to consider, and both suggest compromise as a positive-sum resolution to the AI race.
Risk-neutral value systems
Consider an AI race between eudaimonia maximizers and paperclip maximizers, with odds of winning p and 1-p respectively. If these factions are risk-neutral, then
expected utility of eudaimons = p * utility(resources if win) = utility(p * (resources if win)),
and similarly for the paperclippers. That is, we can pretend for purposes of analysis that when the factions compete for winner-takes-all, they actually control miniature future light cones that are p and 1-p times the size of the whole thing. But some parts of the light cone may be differentially more valuable than others. For example, the paperclippers need lots of planets containing iron and carbon to create steel, while the eudaimons need lots of stars for energy to power their simulations. So the parties would gain from trading with each other: The eudaimons giving away some of their planets in return for some stars. And similarly among other resource dimensions as well.
Risk-averse value systems
For risk-averse agents, the argument for compromise is even stronger. In particular, many egoists may just want to create one immortal copy of themselves (or maybe 5 or 10 for backup purposes); they don't necessarily care about turning the whole future light cone into copies of themselves, and even if they'd like that, they would still probably have diminishing marginal utility with respect to the number of copies of themselves. Likewise for people who care in general about "survival of the human race": It should be quite cheap to satisfy this desire with respect to present-day Earth-bound humans relative to the cosmic scales of resources available. Other ideologies may be risk-averse as well; e.g., negative utilitarians want some computing power to figure out how to reduce suffering, but they don't need vast amounts because they're not trying to fill the cosmos with anything in particular. Even fun theorists, eudaimons, etc. might be satisficing rather than maximizing and exhibit diminishing marginal utility of resources.
In these instances, the case for compromise is even more compelling, because not only can the parties exchange resources that are differentially valuable, but because the compromise also reduces uncertainty, this boosts expected utility in the same way that insurance does for buyers. For instance, with an egoist who just wants one immortal copy of herself, the expected utility of the outcome is basically proportional to the probability that the compromise goes through, which could be vastly higher than her probability of winning the whole light cone. Individual egoists might band together into collective-bargaining units to reduce the transactions costs of making trades with each human separately. This might serve like a group insurance plan, and those people who had more power would be able to afford higher-quality insurance plans.
Carl Shulman has pointed out the usefulness of risk aversion in encouraging cooperation. And indeed, maybe human risk aversion is one reason we see so much compromise in contemporary society. Note that if even only one side is risk-averse, we tend to get very strong compromise tendencies. For example, insurance companies are not risk-averse with respect to wealth (for profits or losses on the order of a few million dollars), but because individuals are, individuals buy insurance, which benefits both parties.
Further market analogies
Just like in a market economy, trade among value systems may include externalities. For instance, suppose that many factions want to run learning computations that include "suffering subroutines," which negative utilitarians would like to avert. These would be analogous to pollution in a present-day context. In a Coase fashion, the negative utilitarians might bargain with the other parties to use alternate algorithms that don't suffer, even if they're slightly costlier. The negative utilitarians could pay for this by giving away stars and planets that they otherwise would have (probabilistically) controlled.
The trade among value systems here has some properties of a market economy, so some of the results of welfare economics will apply. If there are not many buyers and sellers, no perfect information, etc., then the first fundamental welfare theorem may not fully hold, but perhaps many of its principles would obtain in weaker form.
In general, markets are some of the most widespread and reliable instances of positive-sum interaction among competing agents, and we would do well to explore how, why, and when markets work or don't work.
Of course, all of these trade scenarios depend on the existence of clear, robust mechanisms by which compromises can be made and maintained. Such mechanisms are present in peaceful societies that allow for markets, contracts, and legal enforcement, but it's much harder in the "wild west" of AI development, especially if one faction controls the light cone and has no more opposition. Exploring how to make compromise function in these contexts is an urgent research area with the potential to make everyone better off.
Values as vectors
Consider a multi-dimensional space of possible values: Happiness, knowledge, complexity, number of paperclips, etc. Different value systems (axiologies) care about these dimensions to different degrees. For example, hedonistic utilitarians care only about the first and not about the rest. Other people care about each of the first three to some degree.
We can think of a person's axiology as a vector in values space. The components of the vector represent what weight (possibly negative) the person places on that particular value. In a four-dimensional values space of (happiness, knowledge, complexity, paperclips), hedonistic utilitarians have the vector (1, 0, 0, 0). Other people have vectors like (0.94, 0.19, 0.28, 0). Here I've normalized these to unit vectors. To evaluate a given change in the world, the axiologies take the scalar projection of the change onto their vector, i.e., the dot product. For example, if the change is (+2, -1, +1, +4), utilitarians evaluate this as (1, 0, 0, 0) * (2, -1, 1, 4) = 1 * 2 + 0 * -1 + 0 * 1 + 0 * 4 = 2, while the other axiology evaluates its value to be 0.94 * 2 + 0.19 * -1 + 0.28 * 1 + 0 * 4 = 1.97.
We can imagine a similar set-up with the dimensions being policies rather than values per se, with each axiology assigning a weight to how much it wants or doesn't want each policy. This is the framework that Robin Hanson suggested in his post, "Policy Tug-O-War." The figure provides a graphical illustration of a compromise in this setting.

Pareto improvements for competing value systems. The two axiologies are opposed on the x-axis dimension but agree on the y-axis dimension. Axiology #2 cares more about the y-axis dimension and so is willing to accept some loss on the x-axis dimension to compensate Axiology #1.
Sums as compromise solutions?
Adrian Hutter suggested an extension to this formalism: The length of each vector could represent the number of people who hold a given axiology. Or, I would add, in the case of power-weighted compromise, the length could represent the power of the faction. Would the sum of the axiology vectors with power-weighted lengths then represent a natural power-weighted compromise solution? Of course, there may be constraints on which vectors are achievable given resources and other limitations of physical reality.
In some cases, summing axiology vectors seems to give the right solution. For example, consider two completely orthogonal values: Paperclips (x axis) and staples (y axis). Say a paperclip maximizer has twice as much power as its competitor staple maximizer in competing to control Earth's future light cone. The sum of their vectors would be 2 * (1,0) + (0,1) = (2,1). That means 2/3 of resources go to paperclips and 1/3 to staples, just as we might expect from a power-weighted compromise.5
However, imagine now that there's a design for staples that allows paperclips to be fit inside them. This means the staple maximizers could, if they wanted, create some paperclips as well, although by default they wouldn't bother to do so. Assume there is no such design to fit staples inside paperclips. Now the staple maximizers have extra bargaining leverage: "If we get more than 1/3 of resources for staples," they can say, "we'll put some paperclips inside our staples, which will make both of us better off." Here the compromise outcome is based not just on pure power ratios (i.e., probabilities of winning control in a fight) but also on bargaining leverage. This is discussed more in "Appendix: Dividing the compromise pie."
Working together on compromise
I think advancing compromise is among the most important projects that we who want to reduce suffering can undertake. A future without compromise could be many times worse than a future with it. This is also true for other value systems as well, especially those that are risk-averse. Thus, advancing compromise is a win-win(-win-win-win-...) project that many of us may want to work on together. It seems like a robustly positive undertaking, squares with common sense, and is even resilient to changes in our moral outlook. It's a form of "pulling the rope sideways" in policy tug-o-wars.
Acknowledgements
This essay was inspired by a discussion with Lucius Caviola. It draws heavily from the ideas of Carl Shulman. Also influential were writings by Jonah Sinick and Paul Christiano. An email from Pablo Stafforini prompted the section on epistemic convergence.
Appendix: Dividing the compromise pie
Imputations
Consider several factions competing in a winner-takes-all race to control the future light cone. Let pi denote the probability that faction i wins. Normalize the utility values for each faction so that utility of 0 represents losing the light-cone race, and utility of 100 represents winning it. Absent compromise, faction i's expected utility is 100pi. Thus, in order for i to be willing to compromise, it must be the case that the compromise offers at least 100pi, because otherwise it could do better by continuing to fight on its own. Compromise allocations that respect this "individual rationality" requirement are called imputations.
We can see the imputations for the case of deep ecologists and animal welfarists in Figure 2. Absent bargaining, each side gets an expected utility of 100 * 0.5 = 50 by fighting for total control. Bargaining would allow each side to get more than half of what it wants, and the excess value to each side constitutes the gain from compromise.
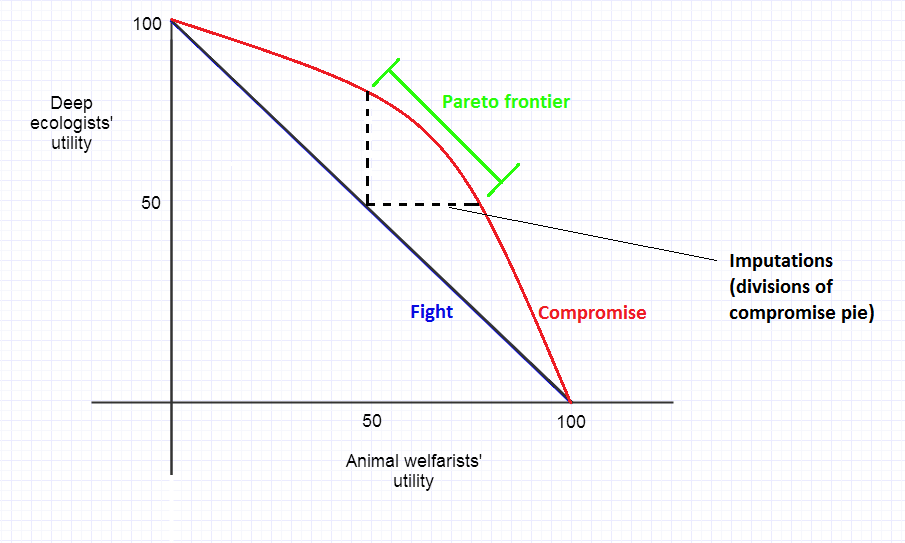
Figure 2: Imputations for compromise between deep ecologists and animal welfarists, with pi = 0.5 for both sides. By "Pareto frontier" in this context, I mean the set of possible Pareto-optimal Pareto improvements relative to to the (50, 50) disagreement point.
As we can see, there may be many imputations for a given problem, and even if they are all individually rational, they may not be collectively stable with more than two players because subgroups of players might gang together to break off from a whole-group compromise. There are various solution concepts for group stability of compromise in cooperative game theory, which impose additional requirements on top of a distribution merely being an imputation.
Compromise pie: Transferable-utility case
Utility is transferable if it can be given to another party without losing any of the value. We can see in Figure 2 that utility is not completely transferable between deep ecologists and animal welfarists, because the Pareto frontier is curved. If the animal welfarists give up 1 unit of expected utility, the deep ecologists may not gain 1 whole unit. Utility would be transferable in the bargaining situation if the Pareto frontier between the two dashed black lines were straight.
In the special case when utility is transferable, we can use all the mechanics of cooperative game theory to analyze the situation. For example, the Shapley value gives an answer to the problem of what the exact pie-slicing arrangement should look like, at least if we want to satisfy the four axioms that uniquely specify the Shapley division.
It's an interesting theorem that if a cooperative game is convex, then all of the players want to work together (i.e., the core is non-empty and also unique), and the Shapley value gives "the center of gravity" of the core. Alas, as far as I can tell, real-world situations will not always be convex.
Non-transferable case: Nash bargaining game
Many times the utility gains from compromise are not completely transferable. We saw this in Figure 2 through the fact that the Pareto frontier is curved. Define u := (animal-welfarist expected utility) - 50, i.e., the excess expected utility above no compromise, and v := (deep-ecologist expected utility) - 50. The (u,v) points that lie within the dotted lines and the curved red line are the potential imputations, i.e., ways to divide the gains from trade. That utility is not transferable in this case means we can't represent the Pareto frontier by a line u + v = constant.
However, we can use another approach, called the Nash bargaining game. In Nash's solution, the bargaining point is that which maximizes u * v. Figure 304.1 (p. 304) of A Course in Game Theory by Osborne and Rubinstein illustrates this graphically as the intersection of lines u * v = constant with set of imputations, and I've drawn a similar depiction in Figure 3:

Figure 3: Nash bargaining solution for 50-50 balance of power.
Note that the split would be different for a differently shaped Pareto frontier. For example, if pdeep ecologists = 0.8 and panimal welfarists = 0.2, then we'd have a situation like the following:
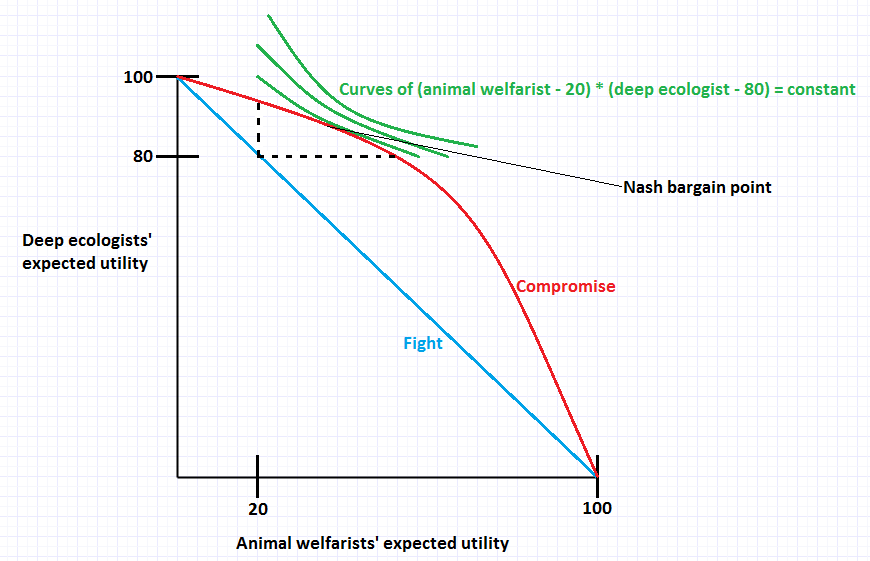
Figure 4: Nash bargaining solution for 80-20 balance of power.
If, for illustration, we use the formula (deep ecologists' expected utility) = 100 - (animal welfarists' expected utility)2/100 for the Pareto frontier, as in Figure 1, then we can compute the exact Nash compromise point, as is shown in the following table:
| Animal welfarists' expected utility | Deep ecologists' expected utility | Animal welfarists' expected utility - 20 | Deep ecologists' expected utility - 80 | (Animal welfarists' expected utility - 20) * (Deep ecologists' expected utility - 80) |
| 20 | 96 | 0 | 16 | 0 |
| 22 | 95.16 | 2 | 15.16 | 30.32 |
| 24 | 94.24 | 4 | 14.24 | 56.96 |
| 26 | 93.24 | 6 | 13.24 | 79.44 |
| 28 | 92.16 | 8 | 12.16 | 97.28 |
| 30 | 91 | 10 | 11 | 110 |
| 32 | 89.76 | 12 | 9.76 | 117.12 |
| 34 | 88.44 | 14 | 8.44 | 118.16 |
| 36 | 87.04 | 16 | 7.04 | 112.64 |
| 38 | 85.56 | 18 | 5.56 | 100.08 |
| 40 | 84 | 20 | 4 | 80 |
| 42 | 82.36 | 22 | 2.36 | 51.92 |
| 44 | 80.64 | 24 | 0.64 | 15.36 |
| 44.72 | 80 | 24.72 | 0 | 0 |
The maximum of the product in the last column occurs around (34, 88), which will be the Nash compromise arrangement. The animal welfarists got a surplus of 34 - 20 = 14, and the deep ecologists, 88 - 80 = 8.
It's worth noting that in fact any of the divisions in the table is a Nash equilibrium, because given the demand of one faction for a share of the pie, the other faction can only either (1) take less, which it wouldn't want to do, or (2) demand more and thereby ruin the compromise, leaving it with no surplus. Thus, the bargaining solution allows us to narrow down to a particular point among the infinite set of Nash equilibria.
The bargaining game contains other solutions besides Nash's that satisfy different intuitive axioms.
Multiple factions with non-transferable utility
The bargaining problem with more than two players becomes more complicated. In "A Comparison of Non-Transferable Utility Values," Sergiu Hart identifies three different proposals for dividing the compromise pie -- Harsanyi (1963), Shapley (1969), and Maschler and Owen (1992) -- each of which may give different allocations. Each proposal has its own axiomatization (see endnote 1 of Hart's paper), so it's not clear which of these options would be chosen. Perhaps one would emerge as a more plausible Schelling point than the others as the future unfolds. ↩ ↩
Footnotes
- Robot animals would represent an improvement, though they aren't a perfect solution because the robots too would probably suffer to some degree in order to operate successfully in the world. That said, perhaps more humane algorithms could be designed than what are used in animals. Also, absence of predators would eliminate the pain of being eaten alive, as well as fear of being eaten. If the robots didn't compete for shared resources, arms-race pressures for intelligence would abate, so the robots would be able to accomplish similar tasks as their biological versions with less cognitive and emotional sophistication. Alas, not everyone would be content with a proposal to replace animals by robot counterparts. In Consciousness Explained (p. 452), Daniel Dennett says that he's glad to know that there are predators in his woods, even if he doesn't see them, and that he would be less satisfied with "robot beasties". (back)
- Depending on what landscape of payoffs is involved, it seems plausible that cooperation could indeed be an evolutionarily stable strategy (ESS). As an example, consider the classic game of hawk-dove with an additional mutant variant, called Own-cooperator, which fights Hawks and Doves but compromises with its own kind. Let the hawk-dove payoffs be V=2 and C=4.
Hawk Dove Own-cooperator Hawk -1, -1 2, 0 -1, -1 Dove 0, 2 1, 1 0, 2 Own-cooperator -1, -1 2, 0 1, 1 Here, Own-cooperation is an ESS using the first condition of Maynard Smith and Price: For the strategy S = Own-cooperator, for any T in {Hawk, Dove}, playing S against S is strictly better than playing T against S. (back)
- In fairness, at bottom Bayesian priors are no different, but some priors seem more "reasonable" than others, at least given certain priors for reasonableness. (back)
- It turns out there's an existing thought experiment with the same name, which is similar in spirit. (back)
- Actually, for completely mutually exclusive values and risk-neutral actors, there are no strict gains from compromise, because the paperclip and staple maximizers are indifferent between a guaranteed 2/3 : 1/3 split vs. 2/3 : 1/3 probabilities of winning everything. Also note that the vector formalism doesn't encapsulate risk-averse value systems or value systems whose axiology is anything other than a linear sum of components. (back)